5 логичких загонетки за проналажење образаца

Уместо знака питања, круг треба да садржи број 253. То је принцип по којем се формирају бројеви у круговима: сваки претходни се помножи са 2, а резултат се дода 3.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Или ево још једног решења: сваком претходном броју се у н-ти степен додаје 2.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Уместо знака питања, на углу треба да стоји слово „П“. Збир бројева у сваком квадрату је редни број слова у абецеди. Хајде да проверимо:

6 + 4 + 4 = 14. „М“ је четрнаесто слово у абецеди. Рачунамо и „Јо“!
4 + 1 + 7 = 12. „К“ је дванаесто слово у абецеди.
5 + 6 + 10 = 21. „У“ је двадесет прво слово у абецеди.
1 + 14 + 2 = 17. „П“ је седамнаесто слово у абецеди, које би требало да буде уместо знака питања.

Уместо знака питања, требало би да стоји број 179. Ако се крећете у смеру казаљке на сату почев од 3, тада је сваки следећи број једнак двоструком броју претходног, коме су додани 1, 3, 5, 7, 9.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

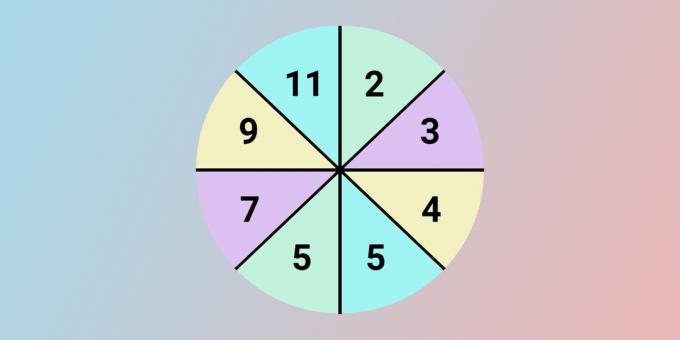
Уместо знака питања, треба да стоји број 11. Да бисмо добили сваки број из леве половине круга, узимамо број из супротног сектора, удвостручујемо и додајемо један.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Уместо знака питања, број треба да буде 66. Ако се крећете у смеру казаљке на сату почев од 4, сваки следећи број једнак је двоструком броју претходног, од којег су одузета два.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.